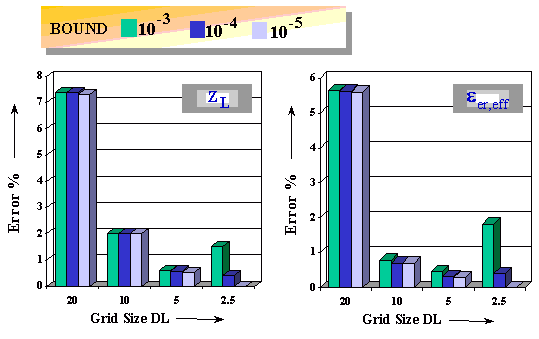
Figure 2-7. Influence of the grid size DL (in mm) and the iteration error BOUND on simulation accuracy by the calculation of coplanar line characteristics
| [close window] | [2.7 Losses] |
The integration of the FDM into CAD software and the intensively use of these programs makes it necessary to investigate some properties of the simulator, like the numerical stability, accuracy setting and convergence behavior. On one hand this will help the user to minimize computation time and to optimize the numerical results. On the other hand the series of simulations will be used for the automation of some model parameters, like the discretization or the iteration boundary. The following calculations were made for a GaAs substrate (er=12.9) with a thickness of 500mm. For explaining the investigations, the coplanar transmission line model was used, which has the advantage of a simple geometry.
At first the influence of two numerical parameters, the grid size DL and the iteration error BOUND on accuracy of the simulation results for a coplanar line are investigated. A coplanar line configuration with the following parameters has been chosen to ensure, that the grid crossings are always on the edges of the metallization: Substrate height h=500mm, er=12.9, w=50mm, s=40mm with a metalization of gold and a thickness of t=3mm. Figure 2-7 depicts the calculation of the line characteristics and its relative error as a function of grid size DL and iteration error BOUND. The relative error decreases with smaller size of DL, whereas the iteration error BOUND has no significant effect as long as the grid size is not too small (here DL³5 mm). For very fine grid (DL£2.5) there is an influence of the iteration error on results.

The two following statements describe the relation of the discretization size and the iteration error in a basic formulation:
The calculations of very small and wide coplanar lines have been evaluated to achieve common statements for the convergence behavior of the simulator. One can obtain a relative error, which is always lower than 1%, if the iteration error is 10-3 and the cell size DL is lower than the smallest line dimension divided by 4. For a fast simulation run or a big number of calculations (e.g. during an optimization), a coarse discretization (the smallest line dimension divided by 2) is already sufficient.
- An decrease of the iteration error does not lead to a better simulation result, if a coarse discretization size is used.
- A large iteration error leads to a poor calculation result, if a very small discretization size is used.
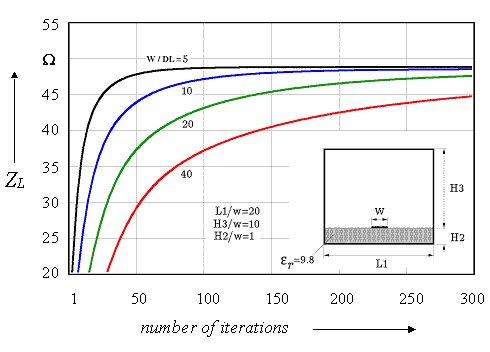
Further convergence investigations proof, that even for very fine grid (smallest line dimension divided by 64) and small iteration error (10-6) the simulator is numerically stable. Figure 2-8 shows the effect of grid size by the calculation of a microstrip line impedance. The calculation time rises from some milliseconds up to 15 minutes (on a workstation HP9000, 160MHz, PA 8000).